Hình thang vuông được sử dụng trong bộ môn Toán hình học. Vậy liệu các bạn có còn nhớ tính chất hình thang vuông? Hãy cùng Gocbao ôn tập lại kiến thức này nhé!
Định nghĩa hình thang vuông
Hình thang là gì?
Hình thang là một tứ giác lồi có hai cạnh đối song song. Hai cạnh song song này được gọi là hai cạnh đáy. Hai cạnh còn lại gọi là hai cạnh bên.
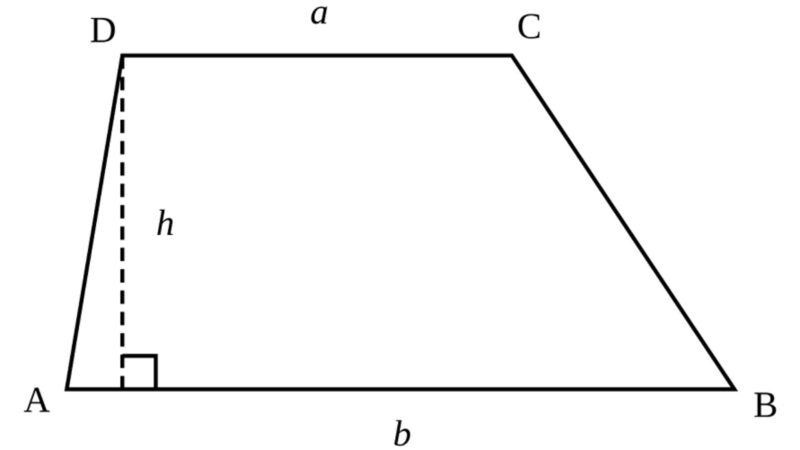
Các trường hợp đặc biệt của hình thang là:
Hình thang vuôngHình thang cânHình thang vuông cân hay còn được gọi là hình chữ nhật
Trong thực tế ta có thể dễ nhận thấy minh họa về hình thang nhất là hình cây thang hoặc những chiếc bàn có mặt bàn hình thang.
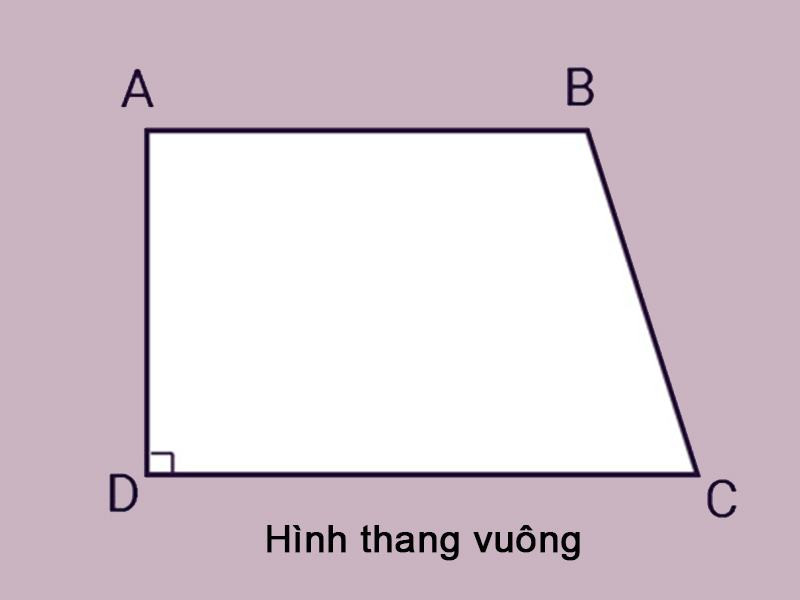
Hình thang vuông là gì?
Hình thang vuông là hình thang có một góc vuông (90°). Nói cách khác, hình thang vuông là một trường hợp đặc biệt của hình thang.
Tính chất hình thang vuông và dấu hiệu nhận biết hình thang vuông
Tính chất hình thang vuông
Hình thang vuông có hai cạnh đáy song song và vuông góc với hai đáy, tạo nên góc 90 độ.
Dấu hiệu nhận biết hình thang vuông
Dấu hiệu để nhận biết hình thang vuông đó chính là hình thang có một góc vuông. Đáp ứng điều kiện này thì tứ giác là hình thang vuông.
Công thức liên quan đến tính chất hình thang vuông
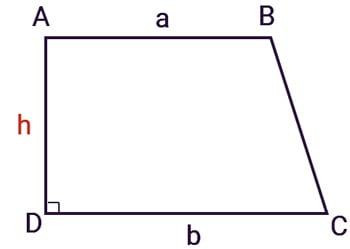
Công thức tính diện tích hình thang vuông
Diện tích hình thang vuông bằng một nửa tích của tổng hai đáy và chiều cao ứng với cạnh đáy hoặc bằng tích của đường cao và trung bình cộng của hai đáy.
S = ½ h . (a + b)
Trong đó:
a, b: Độ dài 2 đáy của hình thangh: Độ dài đường cao (chính là cạnh vuông góc với 2 cạnh đáy)
Công thức tính chu vi hình thang vuông
Chu vi hình thang vuông bằng tổng của hai cặp cạnh.
P = a + b + c + d
Trong đó: a, b, c, d là độ dài các cạnh đáy và các cạnh bên của hình thang vuông.
Chủ đề liên quan:
Tính chất đường phân giác trong tam giác? Lý thuyết & bài tậpTính chất cơ bản của phân thức là gì? 3 Dạng toán cơ bản của phân thức
Các dạng bài tập liên quan đến tính chất hình thang vuông
Bài tập 1
Hình thang vuông ABCD (AB//CD) có AB = 3cm, CD = 6cm, và AD = 4cm. Tính diện tích hình thang ABCD.
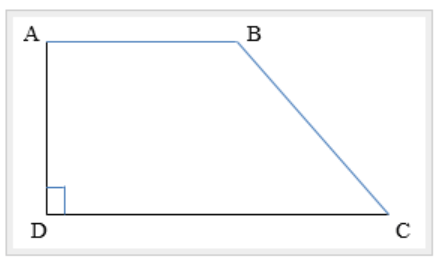
Lời giải:
Hình thang ABCD có AB // CD nên hai đáy là AB, CD
AD ⊥ DC
Suy ra, AD là chiều cao của hình thang.
Áp dụng công thức: S = ½ h . (a + b) = ½ . 4 . ( 3 + 6) = 18 (cm²)
Vậy diện tích của hình thang ABCD là 18cm².
Bài tập 2
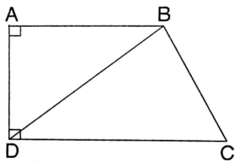
Cho hình thang vuông ABCD có AD = 6cm; DC = 12cm; AB = 2/3 DC
a) Tính diện tích hình thang ABCD?
b) Khi kéo dài cạnh bên AD và CB thì 2 cạnh bên này cắt nhau tại M. Tính độ dài cạnh AM?
Lời giải:
a) Độ dài cạnh AB là:
AB = 2/3 DC = 12 . (2/3) = 8cm
Diện tích ABCD : (8 + 12) / 2 . 6 = 60cm
b) Xét tam giác ABC đáy AB và DBC đáy CD có chiều cao bằng nhau và bằng 6cm, đáy AB = 2/3 CD => S ABC = 2/3 S DBC
Xét tiếp hai tam giác ABC và DBC đáy BC vì S ABC = 2/3 S DBC => AK = 2/3 DH
Xét tiếp tam giác AMC và tam giác DMC chung đáy MC mà chiều cao AK = 2/3 DH => SAMC = 2/3 S DMC
S DMC lớn hơn S AMC (12 . 6) / 2 = 36 cm²
S AMC = 36 / (3 – 2). 2 = 72 (cm²)
Xét tam giác AMC đáy AM, chiều cao CD => AM = 72 . 2 / 12 = 12 (cm)
Vậy độ dài cạnh AM là 12cm.
Bài tập 3
Mảnh đất hình thang có đáy lớn là 38m và đáy bé là 28m. Mở rộng hai đáy về bên phải của mảnh đất với đáy lớn thêm 9m và đáy bé thêm 8m thu được mảnh đất hình thang mới có diện tích lớn hơn diện tích mảnh đất hình thang ban đầu là 107,2 m². Hãy tính diện tích mảnh đất hình thang ban đầu.
Lời giải:
Phần diện tích tăng thêm chính là diện tích của hình thang có đáy lớn bằng 9m và đáy bé là 8m, chiều cao bằng với chiều cao hình thang ban đầu.
Vậy chiều cao mảnh đất này sẽ là:
h = (107,1 x 2) / (9 + 8) = 12,6m
Diện tích mảnh đất hình thang ban đầu là:
S = [(38 + 28) / 2] x 12,6 = 415,8 (m²)
Vậy diện tích mảnh đất hình thang ban đầu là 415,8 m².
Qua bài viết trên, chúng ta đã biết được tính chất hình thang vuông và dấu hiệu để có thể nhận biết hình thang vuông. Gocbao hi vọng rằng các bạn đọc giả đã bổ sung thêm được một kiến thức Toán học thú vị nữa.

